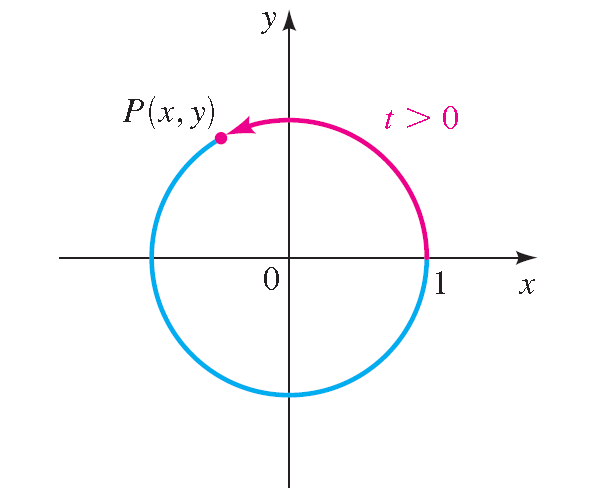
Suppose t is a real number. Let’s mark off a distance t along the unit circle, starting at the point (1, 0) and moving in a counterclockwise direction, if t is positive or in a clockwise direction, if t is negative.
In this way we arrive at a point P(x, y) on the unit circle. The point P(x, y) obtained in this way is called the terminal point determined by the real number t.
Terminal Point P(x, y) Determined by t > 0 :
Terminal Point P(x, y) Determined by t < 0 :
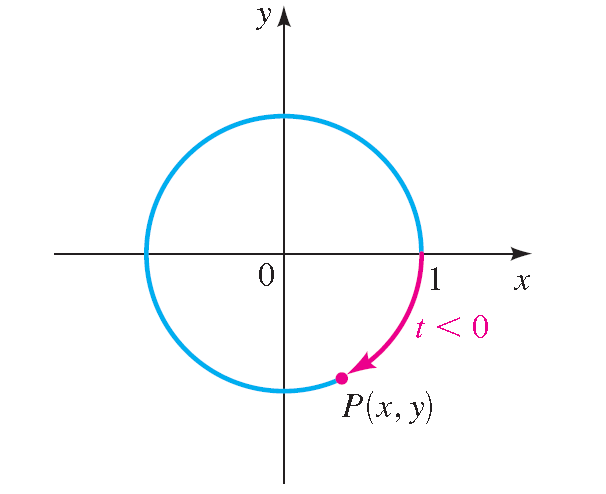
The circumference of the unit circle is
S o, if a point starts at (1, 0) and moves counter clockwise all the way around the unit circle and returns to (1, 0), it travels a distance of 2 π . To move halfway around the circle, it travels a distance of (1/2)(2 π) = π.
To move a quarter of the distance around the circle, it travels a distance of (1/4)(2 π) = π/2. W here does the point end up when it travels these distances along the circle? In the diagram shown below, we see, for example, that when it travels a distance of π starting at (1, 0), its terminal point is (-1, 0).
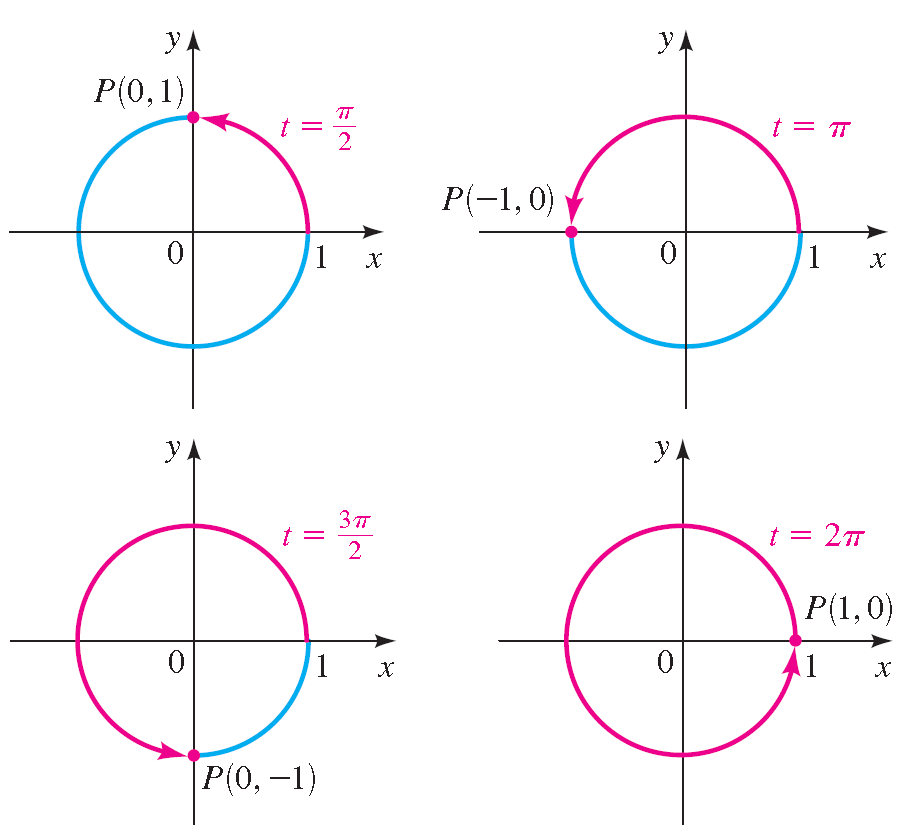
Find the terminal point on the unit circle determined by each real number t.
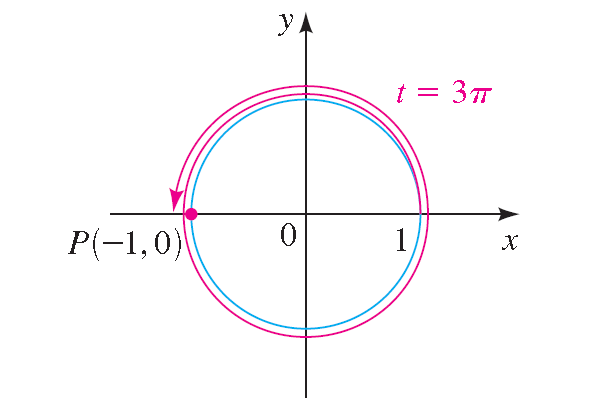
The terminal point determined by 3 π is (-1, -0).
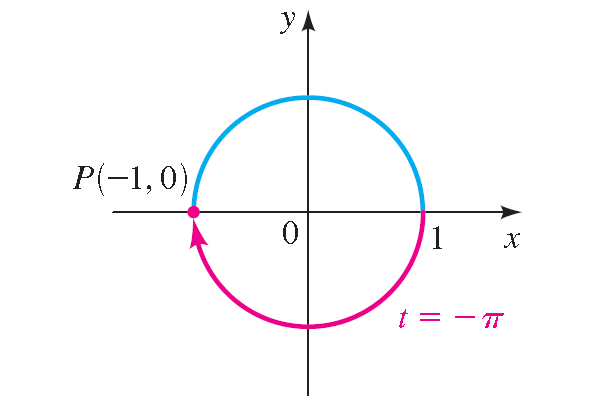
The terminal point determined by - π is (-1, -0).
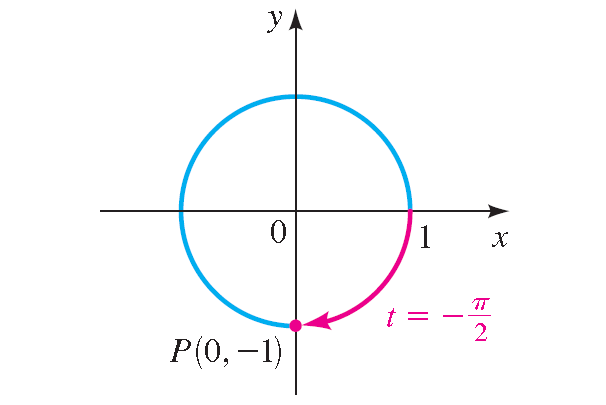
The terminal point determined by - π/2 is (0, -1).
Notice that different values of t can determine the same terminal point.
The terminal point P(x, y) determined by t = π /4 is the same distance from (1, 0) as from (0, 1) along the unit circle.
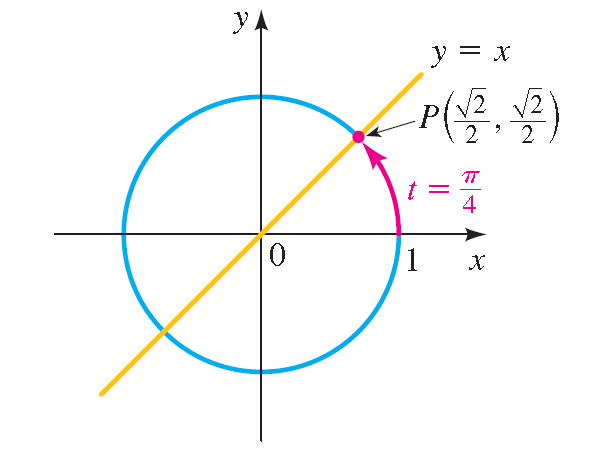
Since the unit circle is symmetric with respect to the line y = x, it follows that P lies on the line y = x. So P is the point of intersection (in the first quadrant) of the circle x 2 + y 2 = 1 and the line y = x.
Substituting x for y in the equation of the unit circle.
Because P is in the first quadrant, x = 1/ √ 2 and y = x, we have y = 1/ √ 2 also.
Thus the terminal point determined by π/4 is
P(1/ √ 2, 1/ √ 2) = P( √ 2/2, √ 2/2)
Similar methods can be used to find the terminal points determined by t = π/6 and t = π/3.